Отклонение относительных показателей

Что такое стандартное отклонение — использование функции СТАНДОТКЛОН для расчета стандартного отклонения в Excel

Стандартное отклонение является одним из тех статистических терминов в корпоративном мире, которое позволяет поднять авторитет людей, сумевших удачно ввернуть его в ходе беседы или презентации, и оставляет смутное недопонимание тех, кто не знает, что это такое, но стесняется спросить. На самом деле большинство менеджеров не понимают концепцию стандартного отклонения и, если вы один из них, вам пора перестать жить во лжи. В сегодняшней статье я расскажу вам, как эта недооцененная статистическая мера позволит лучше понять данные, с которыми вы работаете.

Что измеряет стандартное отклонение?

Представьте, что вы владелец двух магазинов. И чтобы избежать потерь, важно, чтобы был четкий контроль остатков на складе.

В попытке выяснить, кто из менеджеров лучше управляет запасами, вы решили проанализировать стоки последних шести недель.

Средняя недельная стоимость стока обоих магазинов примерно одинакова и составляет около 32 условных единиц. На первый взгляд среднее значение стока показывает, что оба менеджера работают одинаково.

[attention type=yellow]

Но если внимательнее изучить деятельность второго магазина, можно убедится, что хотя среднее значение корректно, вариабельность стока очень высокая (от 10 до 58 у.е.). Таким образом, можно сделать вывод, что среднее значение не всегда правильно оценивает данные. Вот где на выручку приходит стандартное отклонение.

[/attention]

Стандартное отклонение показывает, как распределены значения относительно среднего в нашей выборке.  Другими словами, можно понять на сколько велик разброс величины стока от недели к неделе.

В нашем примере, мы воспользовались функцией Excel СТАНДОТКЛОН, чтобы рассчитать показатель стандартного отклонения вместе со средним.

В случае с первым менеджером, стандартное отклонение составило 2. Это говорит нам о том, что каждое значение в выборке в среднем откланяется на 2 от среднего значения. Хорошо ли это? Давайте рассмотрим вопрос под другим углом – стандартное отклонение равное 0, говорит нам о том, что каждое значение в выборке равно его среднему значению (в нашем случае, 32,2).

Так, стандартное отклонение 2 ненамного отличается от 0, и указывает на то, что большинство значений находятся рядом со средним значением. Чем ближе стандартное отклонение к 0, тем надежнее среднее. Более того, стандартное отклонение близкое к 0, говорит о маленькой вариабельности данных.

То есть, величина стока со стандартным отклонением 2, указывает на невероятную последовательность первого менеджера.

В случае со вторым магазином, стандартное отклонение составило 18,9. То есть стоимость стока в среднем отклоняется на величину 18,9 от среднего значения от недели к неделе.

Сумасшедший разброс! Чем дальше стандартное отклонение от 0, тем менее точно среднее значение. В нашем случае, цифра 18,9 указывает на то, что среднему значению (32,8 у.е. в неделю) просто нельзя доверять.

[attention type=red]

Оно также говорит нам о том, что еженедельная величина стока обладает большой вариабельностью.

[/attention]

Такова концепция стандартного отклонения в двух словах. Хотя оно не дает представление о других важных статистических измерениях (Мода, Медиана…), фактически стандартное отклонение играет решающую роль в большинстве статистических расчетов. Понимание принципов стандартного отклонения прольет свет на суть многих процессов вашей деятельности.

Как рассчитать стандартное отклонение?

Итак, теперь мы знаем, о чем говорит цифра стандартного отклонения. Давайте разберемся, как она считается.

Рассмотрим набор данных от 10 до 70 с шагом 10. Как видите, я уже рассчитал для них значение стандартного отклонения с помощью функции СТАНДОТКЛОН в ячейке H2 (оранжевым).

Ниже описаны шаги, которые предпринимает Excel, чтобы прийти к цифре 21,6.

Обратите внимание, что все расчеты визуализированы, для лучшего понимания. На самом деле в Excel расчет происходит мгновенно, оставляя все шаги за кулисами.

Для начала Excel находит среднее значение выборки. В нашем случае, среднее получилось равным 40, которое на следующем шаге отнимают от каждого значения выборки. Каждую полученную разницу возводят в квадрат и суммируют.

У нас получилась сумма равная 2800, которую необходимо разделить на количество элементов выборки минус 1. Так как у нас 7 элементов, получается необходимо 2800 разделить на 6.

Из полученного результата находим квадратный корень, это цифра будет стандартным отклонением.

Для тех, кому не совсем ясен принцип расчета стандартного отклонения с помощью визуализации, привожу математическую интерпретацию нахождения данного значения.

Функции расчета стандартного отклонения в Excel

В Excel присутствует несколько разновидностей формул стандартного отклонения. Вам достаточно набрать =СТАНДОТКЛОН и вы сами в этом убедитесь.

Стоит отметить, что функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г (первая и вторая функция в списке) дублируют функции СТАНДОТКЛОН и СТАНДОТКЛОНП (пятая и шестая функция в списке), соответственно, которые были оставлены для совместимости с более ранними версиями Excel.

Вообще разница в окончаниях .В и .Г функций указывают на принцип расчета стандартного отклонения выборки или генеральной совокупности. Разницу между двумя этими массивами я уже объяснял в предыдущей статье расчета дисперсии.

[attention type=green]

Особенностью функций СТАНДОТКЛОНА и СТАНДОТКЛОНПА (третья и четвертая функция в списке), является то, что при расчете стандартного отклонения массива в расчет принимаются логические и текстовые значения.

[/attention]

Текстовые и истинные логические значения равняются 1, а ложные логические значения равняются 0.

Мне трудно представить ситуацию, когда бы мне могли понадобится эти две функции, поэтому, думаю, что их можно игнорировать.

Вам также могут быть интересны следующие статьи

Источник: https://exceltip.ru/%D1%87%D1%82%D0%BE-%D1%82%D0%B0%D0%BA%D0%BE%D0%B5-%D1%81%D1%82%D0%B0%D0%BD%D0%B4%D0%B0%D1%80%D1%82%D0%BD%D0%BE%D0%B5-%D0%BE%D1%82%D0%BA%D0%BB%D0%BE%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5-%D0%B8%D1%81%D0%BF/

Как найти относительное изменение в процентах

Как рассчитать абсолютное отклонение за 2 года в таблице?

Примеры расчетов, как все сделать, придерживаясь плана?

Абсолютное отклонение: что это такое и как его рассчитать?

Абсолютное отклонение — это различие в показателях отчетного или текущего периодов и любого другого прошедшего периода. Оно вычисляется для того, чтобы выяснить, насколько рентабельно предприятие.

Для расчета берутся два показателя (данные двух периодов или запланированные и фактические показатели), из них выбирается большее, а затем из него вычитают меньшее. Если налицо фактическое повышение оборота, то значение записывают со знаком «+», если уменьшение — соответственно, с «-«.

Относительное отклонение: что это и как оно рассчитывается?

По сути, относительное отклонение — это то же абсолютное, однако оно выражено уже не в конкретных числах, а в процентах. При этом значение на выходе всегда будет положительным.

Как найти относительное отклонение? Мы берем показатель текущего периода (или фактический показатель) и делим его на показатель более раннего периода (или планового), умножаем полученное значение на 100 и вычитаем 100.

3.3. Абсолютные и относительные отклонения

Абсолютное отклонение – это разность между фактической и базовой величиной показателя. Абсолютные отклонения могут быть рассчитаны для любых количественных и качественных показателей (объема продукции, количественных и качественных показателей, характеризующих использование ресурсов, величины активов, прибыли, финансовых коэффициентов и т. п.). Например,

среднесписочная численность работающих;

выработка продукции на одного работающего.

Базовые значения показателей в анализе принято обозначать индексом 0, фактические – 1, отклонения (изменения) – символом ?.

Относительное отклонениепозволяет измерить прирост ресурса с учетом темпов роста продукции, выпущенной с использованием данного ресурса. Относительные отклонения вычисляются только для количественных показателей, характеризующих величину потребленных ресурсов (затрат ресурсов).

Чтобы найти относительное отклонение, нужно из фактической величины ресурса вычесть его базовую величину, скорректированную на коэффициент изменения объема продукции.

Величина R0 ? k N показывает, сколько ресурсов было бы необходимо для производства фактического объема продукции, если бы не изменялись качественные характеристики использования ресурсов.

Отрицательное относительное отклонение называется относительной экономией ресурса, положительное – относительным перерасходом.

Если представить фактическую величину ресурса через его базовую величину и темп роста, формулу исчисления относительного отклонения можно преобразовать следующим образом:

Такое представление демонстрирует, что относительное отклонение возникает за счет разницы темпов роста ресурса и продукции.

Если темп роста продукции опережает темп роста ресурса, возникает относительная экономия, что свидетельствует о достаточно эффективном использовании ресурса.

[attention type=yellow]

Если же темп роста ресурса превышает темп роста продукции, ресурс используется неэффективно, о чем свидетельствует относительный перерасход.

[/attention]

Если же темпы роста ресурса и продукции совпадают, относительное отклонение равно нулю. Это означает, что прирост продукции получен экстенсивным путем, т. е. только за счет привлечения дополнительных ресурсов. При этом качественные показатели использования ресурса не изменяются.

На основании данных таблицы 3.1 оценим эффективность использования трудовых ресурсов.

Исходные данные для оценки эффективности использования трудовых ресурсов

Как правильно рассчитать отклонение, и для чего это нужно

Для эффективного анализа данных и для нахождения проблемных участков в производстве необходимо находить отклонения в показателях. Отклонения бывают нескольких видов и отличаются как единицами измерения, так и способом получения, среди них можно выделить:

• Стандартное отклонение;
• Абсолютное отклонение;
• Относительное отклонение;
• Селективное отклонение;
• Кумулятивное отклонение;
• Отклонение во временном разрезе.

Как рассчитать отклонение в каждом случае, вы узнаете из этой статьи.

Как определить динамику изменения значений при отклонении

Нередко для того, чтобы понять насколько плавно изменяется тот или иной показатель на нескольких отрезках времени, простого среднего значения, сравниваемого с наименьшим или наибольшим числом из ряда – недостаточно. В таких случаях для более глубоко анализа применяется нахождение стандартного отклонения, показывающего более четко динамику изменения значений.

Даны показатели затрат на средства уборки для двух заведений: 10, 21, 49, 15, 59 и 31, 29, 34, 27, 32, где средним значением будет 30,8 и 30,6.

Показатели в среднем приблизительно одинаковы, однако даже визуально видно, что значения в одном заведении изменяются не равномерно, что их контроль производится от случая к случаю. Но для более полного представления необходимо найти стандартное отклонение. Оно будет равно: 19,51 и 2,4.

При среднем значении в первом заведении 30,8 показатели отклоняются от него более чем существенно – 21,8, соответственно у вас есть подтверждение небрежного отношения к работе.

Рассчитывается оно следующим образом:

1. Необходимо рассчитать среднее значение для проверяемого ряда данных. (10+21+49+15+59)/5=30,8
2. Найти разницу между каждым показателем и средним значением. 10-30,8=-20,8; 21-30,8=9,8; 49-30,8=18,2; 15-30,8=15,8; 59-30,8=28,2
3. Возвести каждое значение разницы в квадрат.

   -20,82=432,64; 9,82=96,04; 18,22=331,24; 15,82=249,64; 28,22=795,24.

4. Сложить полученные результаты. 432,64+96,04+331,24+249,64+795,24=1904,8
5. Полученный результат делиться на количество значений в ряду.

   1904,8/5=380,96

6. Корень из полученного числа и будет средним отклонением ?380,96=19,51

Обязательный минимум

Под понятием абсолютного отклонения принято подразумевать отличия одного показателя от другого в числовом значении. Например, разница выручки за два дня: 15-13=2, где 2 – абсолютное отклонение. Этот способ подходит для нахождения отклонения между фактическим и планируемым результатом.

Для правильного выбора уменьшаемого и вычитаемого, необходимо четко понимать, для чего находится отклонения, например в случае с прибылью, планируемая будет уменьшаемым, а фактическая – вычитаемым. Использование абсолютного отклонения редко помогает при глубоком анализе ситуации.

Процент воспринимается лучше

Относительным отклонением считают процентное отношение одного показателя к другому.

Чаще всего его рассчитывают для понимания того, как тот или иной компонент относится к целому значению ли параметру, а также для нахождения отношения между планируемым показателем и фактическим.

[attention type=red]

Это помогает найти отношение затрат на транспортировку к сумме всех затрат, или объясняет, как в процентах относится полученная выручка к планируемой.

[/attention]

Применение относительного отклонения позволяет повысить уровень наглядности проводимого анализа, что в свою очередь дает возможность более точно вычленить и оценить произошедшие в системе изменения.

Как это поможет в сезонной работе

Селективное отклонение призвано помочь сравнить исследуемые данные за определенные промежутки времени. Данным отрезком времени могут быть кварталы, месяцы, не редко это сравнения дней.

И для большей информативности необходимо сравнивать временные отрезки не в пределах одного года, а с такими же за прошлые года.

Это более точно покажет общую тенденцию изменений величин на протяжении нескольких лет и поможет четче выявить влияющие на них факторы.

Наибольшую актуальность применение селективного отклонения находит в фирмах, доход которых неравномерно распределен на протяжении года. То есть поставщики сезонных продуктов или услуг.

Как выявить тренд отклонения

Сумма, исчисляемая нарастающим итогом, называется кумулятивным отклонением. Благодаря ему производится оценка параметра, его рост или падение за заданный промежуток времени, чаще всего месяц. А также позволяет спланировать конечный результат изменений за период.

Благодаря этому можно игнорировать случайные, несистематические изменения параметра, не влияющие на долгосрочную перспективу (весь период) и давать более четкую тенденцию движения параметра.

Она чаще всего показывается в виде прямой на графике, последовательно отмечающем все показатели параметра, и соединяющей начальную и конечную точки ломаной линии. Ее направление вниз или вверх и будет тенденцией.

Отклонение во временном разрезе

Зачастую с его помощью происходит сравнение фактического и планируемого показателя. Является крайне важным в случае негативного отклонения планового значения от фактического. Позволяет использовать в анализе реальный результат вместо планируемого или желаемого показателей.

Формула процентного изменения в Excel

Формула процентного изменения очень часто используется в Excel. Например, чтобы вычислить ежемесячное или общее изменение.

Ежемесячное изменение

1. Выберите ячейку C3 и введите формулу, показанную ниже.
2. Выберите ячейку C3 и примените к ней процентный формат.
3. Чтобы не повторять 1-й и 2-й шаг еще десять раз, выделите ячейку C3, нажмите на ее правый нижний угол и перетащите его вниз до ячейки С13.
4. Проверьте, всели прошло хорошо.

Общее изменение

1. Аналогичным образом, мы можем вычислить общее изменение. На этот раз зафиксируем ссылку на ячейку В2. Выделите ячейку D3 и введите формулу, показанную ниже.
2. Выберите ячейку D3 и применить к ней процентный формат.
3. Выделите ячейку D3, нажмите на ее правый нижний угол и перетащите его вниз до ячейки D13.
4. Проверьте, всели прошло хорошо.

Объяснение: Когда мы протягиваем (копируем) формулу вниз, абсолютная ссылка ($B$2) остается неизменной, а относительная (B3) изменяется – B4, B5, B6 и т.д.

Возможно, этот пример слишком сложен для вас на данном этапе, но он показывает несколько полезных и мощных возможностей, которыми располагает Excel.

Статья написана по материалам сайтов: studfiles.net, finrussia.ru, office-guru.ru.

«

Источник: https://arenaprava.ru/drugoe/kak-najti-otnositelnoe-izmenenie-v-protsentah/

Горизонтальный анализ отчетности

Горизонтальный анализ означает метод сопоставления значений одинаковых показателей в течение определенного временного периода. Другим названием метода является временной или динамичный, ведь проводится оценка изменения в определенном году по сравнению с показателя в предыдущем или базовом.

Горизонтальный анализ подразумевает сопоставление данных одного периода с предыдущим. В рамках финансового горизонтального анализа баланса происходит сравнение значения, например, дебиторской задолженности за 2016 год с дебиторской задолженностью за 2015 год.

Расчет абсолютных и относительных отклонений является важным элементом этого метода. Абсолютное отклонение означает изменение показателя, выраженное в рублях или другой валюте. Относительное отклонение означает изменение показателя, выраженное в процентах.

Простыми словами: Горизонтальный анализ – это сравнение данных за определенный времени.

Горизонтальный анализ, как и вертикальный анализ, также может использоваться при изучении основных форм финансовой отчетности предприятия: баланса, отчета о финансовых результатах, отчета о движении денежных средств. Кроме этого, в процессе анализа следует сравнивать между собой приросты показателей из различных форм финансового отчета, что позволит сформировать дополнительные выводы и рекомендации.

Методика проведения горизонтального анализа отчетности

Процесс предусматривает определение абсолютного отклонения, а также относительного прироста показателя. Например, при определении изменения суммы основных средств формула будет иметь вид:

Абсолютный прирост =

сумма основных средств в текущем году —

— сумма основных средств в предыдущем году

Относительный прирост =

абсолютный прирост

сумма основных средств в предыдущем году

*100%

При исследовании длительных явлений, происходящих в течение трех лет и более, целесообразно применять дефляторы для получения реальных результатов изменения явления в процессе его развития.

При выполнении анализа изменений из года в год, соблюдайте следующие правила:

1. Если элемент имеет значение в базовом году, и не имеет нулевое значение в следующем периоде, снижение равно 100%.

2. Осмысленное процентное изменение не может быть посчитано, если одно число является положительным, а второе число отрицательное.

3. Процентное изменение не может быть вычислено, если нет числа в базовом периоде.

Понимание результатов проведенного горизонтального анализа

Трактовка результатов зависит от явления, которое исследуется. Например, уменьшение стоимости основных средств может быть свидетельством снижения производственного потенциала предприятия, т.е. является негативным явлением.

В то же время сокращение объектов незаконченного строительства свидетельствует о введении предприятием новых основных средств в деятельность, т.е. является положительным явлением.

Увеличение суммы собственного капитала приводит к улучшению показателей финансовой устойчивости.

Пример

При изучении финансовой отчетности и коэффициентов также важно определить тенденции, ведь они столь же важны для понимания деятельности компании, как и абсолютные или относительные показатели.

Анализ тенденций дает важную информацию относительно исторических показателей и роста и, учитывая достаточно длинную историю точной сезонной информации, может оказать большую помощь в качестве инструмента планирования и прогнозирования для управленцев и аналитиков.

Таблица 1 – Горизонтальный анализ баланса для гипотетической компании в течение 5 лет, тыс. руб.

Показатели	Период	Абсолютное отклонение	Относительное отклонение
1	2	3	4	5
Основные средства	9	2	6	1	8	-1	-11,1
Внеоборотные активы	9	2	6	1	8	-1	-11,1
Запасы	25	25	36	15	27	2	8
Дебиторская задолженность	67	41	37	44	79	12	17,9
Финансовые вложения	6	7	7	1	4	-2	-33,3
Денежные средства и эквиваленты	19	29	27	39	16	-3	-15,8
Оборотные активы	117	102	107	99	126	-9	-7,7
Активы	126	104	113	100	134	-8	-6,3

Таблица 1 представляет собой частичный баланс для гипотетической компании в течение пяти периодов. В двух последних столбцах таблицы показаны изменения за период №5 по сравнению с периодом 1, что выражается как в абсолютной валюте (в данном случае, в рублях), так и в процентах.

Стоит рассмотреть причины, по которым происходит изменение, что позволит понять тенденции, которые сформировались в компании. В этом примере наибольший процент изменения показывают инвестиции, которые уменьшились на 33,3 процента. Тем не менее, исследование абсолютной валютной суммы изменений показывает, что инвестиции изменились лишь на 2 тыс. руб.

, и более значительным изменением стало увеличение на 12 тыс. руб. дебиторской задолженности.

Горизонтальный анализ балансов выдвигает на первый план структурные изменения, которые произошли в бизнесе. Прошлые тенденции, очевидно, не обязательно являются точным предсказателем будущего, особенно когда происходят экономические или конкурентные изменения окружающей среды.

[attention type=green]

Исследование прошлых тенденций является более ценным, когда макроэкономические условия и конкурентная среда являются относительно стабильными и когда аналитик рассматривает стабильный или зрелый бизнес. Тем не менее, даже в менее стабильных условиях, исторический анализ может служить основой для разработки прогнозов.

[/attention]

Понимание прошлых тенденций является полезным в оценке того, сохранятся ли эти тенденции или изменят свое направление.

Одним из показателей успеха для компании является более быстрый рост по сравнению со скоростью роста рынка, в котором она работает.

Компании, которые растут медленно, могут оказаться не в состоянии привлечь капитал.

С другой стороны, компании, которые растут слишком быстро, могут обнаружить, что их административные и информационные системы управления не могут идти в ногу со скоростью расширения.

Связи между формами финансовой отчетности при горизонтальном анализе

Данные тренда, генерируемые горизонтальным анализом, можно сравнить с другими элементами финансовой отчетности.

Например, темпы роста активов для гипотетической компании в таблице 1 можно сравнить с ростом выручки компании за тот же период времени.

Если доходы растут быстрее, чем активов, то компания повышает свою эффективность (то есть, производит больше выручки на каждый рубль, вложенный в активы).

В качестве еще одного примера рассмотрим ежегодные процентные изменения для гипотетической компании:

Выручка +20%

Чистая прибыль +25%

Операционный денежный поток -10%

Активы +30%

Чистая прибыль растет быстрее, чем выручка, что свидетельствует о растущей рентабельности. Тем не менее, аналитик должен был бы определить, возникли ли более высокие темпы роста чистой прибыли от обычной деятельности или от неосновной деятельности.

Кроме того, снижение на 10 процентов операционного денежного потока, несмотря на рост выручки и чистой прибыли, явно требует дальнейшего расследования, поскольку это может указывать на проблемное качество прибыли. Наконец, тот факт, что активы росли быстрее, чем выручка, показывает снижение эффективности компании.

Аналитик должен изучить факторы увеличения активов и причины этих изменений.

Источники:

Thomas R. Robinson, International financial statement analysis / Wiley, 2008, 188 pp.

[attention type=yellow]

Когденко В.Г., Экономический анализ / Учебное пособие. — 2-е изд., перераб. и доп. — М.: Юнити-Дана, 2011. — 399 с.

[/attention]

Бузырев В.В., Нужина И.П. Анализ и диагностика финансово-хозяйственной деятельности строительного предприятия / Учебник. — М.: КноРус, 2016. — 332 с.

Источник: https://www.finalon.com/ru/metody-analiza/95-horyzontalnyj-analiz

Как рассчитать отклонение

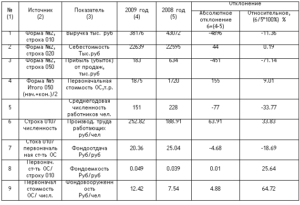
Многие экономисты ломают себе голову над тем, как рассчитать стандартное отклонение и что это такое. Кроме того, им еще нужно знать, что такое абсолютное отклонение и относительное. В этой статье описаны методы расчетов этих отклонений.

Стандартное отклонение

Стандартное отклонение, как рассчитать его? Для начала нужно понять, что же такое стандартное отклонение. Это очень существенный показатель рассеяния в разделе описательной статистики. Стандартное отклонение можно рассчитать по следующему алгоритму:

1. Сначала — вычисление среднего арифметического выборки данных.
2. Затем нужно вычесть среднее арифметическое от каждого элемента выборки.
3. Каждую полученную разницу следует возвести в квадрат.
4. Сложить все квадраты разниц, полученные в пункте 3.
5. Поделить сумму квадратов на количество элементов выборки.
6. Теперь из этого частного нужно извлечь квадратный корень.

Результат, который вы получите, и будет являться стандартным отклонением.

Абсолютное отклонение

Как рассчитать абсолютное отклонение? Абсолютным отклонением можно назвать разницу, получаемую при вычитании одной величины из другой, этот способ является выражением сложившихся положений вещей между плановым и фактическим параметрами.

Известно, что определенную проблему обычно вызывает такой показатель, как знак абсолютного отклонения. Обычно считается, что отклонение, которое позитивно сказывается на прибыли предприятия, считается положительным, и в вычислениях его ставят со знаком «+».

Что же касается банальной математики, такой подход считается не совсем корректным, а это, в свою очередь, вызывает конфликты и разногласия среди специалистов. Исходя из этого, на практике вычисления абсолютного отклонения зачастую пользуются не базовой экономической, а математической моделью.

Математическая модель   заключается в том, что повышение фактического оборота в сравнении с запланированным обозначается знаком «+», а уменьшение фактических издержек в сравнении с плановыми обозначается знаком «-».

Относительное отклонение

Как рассчитать относительное отклонение? Отклонение можно рассчитывать, опираясь на отношение к другим величинам, а это значит, что данный показатель выражается в процентах.

Зачастую относительные отклонения вычисляются по отношению к относительно базовому значению или параметру.

К примеру, можно выразить относительное отклонение, допустим, тех же затрат на материалы, как отношение к суммарной затрате или в проценте к обороту.

В применении относительных отклонений следует учесть, что их наличие способствует повышению уровня информативности анализа, который мы проводим, а следовательно, позволяет более отчетливо оценивать изменение, которое произошло в системе.

Так, можно рассмотреть все на данном примере, возьмём величину абсолютного отклонения оборота, которая будет равна 1000 — 800 = 200.

Данная цифра воспринимается в расчете относительного отклонения не так наглядно, как, к примеру, величина отклонения, показатели в которой выводятся в процентах: (1000 — 800) / 800 * 100% = 25%. Согласитесь, это все-таки режет глаз.

Селективное отклонение

Как рассчитать отклонение такого рода? Этот способ расчета отклонения подразумевает сравнение контролируемых величин на определенном промежутке времени, это может быть такой показатель времени, как квартал или месяц, иногда даже это бывает день.

Сравнивание интересующих нас величин за определенный промежуток времени (к примеру, месяц, давайте возьмем май) текущего года с тем же маем предыдущего года может дать нам  более информативное сравнение с предыдущим месяцем, который рассматривается в плановом периоде.

Селективное отклонение актуальны для фирм, которые занимаются поставкой сезонных услуг. Далее будут описаны еще несколько видов отклонений, знание которых может существенно облегчить вашу жизнь.

Кумулятивное отклонение

Кумулятивным отклонением можно назвать сумму, исчисляемую нарастающим итогом (кумулятивная сумма), и ее отклонение позволяет оценить уровень достижения за определенные периоды (месяцы) или же возможную разницу к окончанию определенного периода.

Возникающее в отдельном периоде случайное колебание параметра деятельности предприятия может привести к значительному отклонению на коротком отрезке времени.

Сама же кумуляция компенсирует случайные отклонения и позволяет более точным образом определить тренд. 

Как посчитать процент отклонения в Excel по двум формулам

Понятие процент отклонения подразумевает разницу между двумя числовыми значениями в процентах. Приведем конкретный пример: допустим одного дня с оптового склада было продано 120 штук планшетов, а на следующий день – 150 штук.

Разница в объемах продаж – очевидна, на 30 штук больше продано планшетов в следующий день. При вычитании от 150-ти числа 120 получаем отклонение, которое равно числу +30.

Возникает вопрос: чем же является процентное отклонение?

Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%. Формулу легко проверить 120+25%=150.

[attention type=red]

Обратите внимание! Если мы старое и новое число поменяем местами, то у нас получиться уже формула для вычисления наценки.

[/attention]

Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2

Важно обратит внимание в данной формуле на наличие скобок. По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания.

Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным.

Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.

Правильно со скобками введите формулу в ячейку D2, а далее просто скопируйте ее в остальные пустые ячейки диапазона D2:D5.

Чтобы скопировать формулу самым быстрым способом, достаточно подвести курсор мышки к маркеру курсора клавиатуры (к нижнему правому углу) так, чтобы курсор мышки изменился со стрелочки на черный крестик.

После чего просто сделайте двойной щелчок левой кнопкой мышки и Excel сам автоматически заполнит пустые ячейки формулой при этом сам определит диапазон D2:D5, который нужно заполнить до ячейки D5 и не более. Это очень удобный лайфхак в Excel.

В альтернативной формуле, вычисляющей относительное отклонение значений продаж с текущего года сразу делиться на значения продаж прошлого года, а только потом от результата отнимается единица: =C2/B2-1.

Как видно на рисунке результат вычисления альтернативной формулы такой же, как и в предыдущей, а значит правильный. Но альтернативную формулу легче записать, хот и возможно для кого-то сложнее прочитать так чтобы понять принцип ее действия. Или сложнее понять, какое значение выдает в результате вычисления данная формула если он не подписан.

[attention type=green]

Единственный недостаток данной альтернативной формулы – это отсутствие возможности рассчитать процентное отклонение при отрицательных числах в числителе или в заменителе. Даже если мы будем использовать в формуле функцию ABS, то формула будет возвращать ошибочный результат при отрицательном числе в заменителе.

[/attention]

Так как в Excel по умолчанию приоритет операции деления выше операции вычитания в данной формуле нет необходимости применять скобки.

Источник:

Как определить динамику изменения значений при отклонении

Нередко для того, чтобы понять насколько плавно изменяется тот или иной показатель на нескольких отрезках времени, простого среднего значения, сравниваемого с наименьшим или наибольшим числом из ряда – недостаточно. В таких случаях для более глубоко анализа применяется нахождение стандартного отклонения, показывающего более четко динамику изменения значений.

Пример:

Даны показатели затрат на средства уборки для двух заведений: 10, 21, 49, 15, 59 и 31, 29, 34, 27, 32, где средним значением будет 30,8 и 30,6.

Показатели в среднем приблизительно одинаковы, однако даже визуально видно, что значения в одном заведении изменяются не равномерно, что их контроль производится от случая к случаю. Но для более полного представления необходимо найти стандартное отклонение. Оно будет равно: 19,51 и 2,4.

При среднем значении в первом заведении 30,8 показатели отклоняются от него более чем существенно – 21,8, соответственно у вас есть подтверждение небрежного отношения к работе.

Источник: https://soveti-masterov.com/instruktsii/kak-rasschitat-otklonenie.html